Algoritma Dijkstra dan Floyd-Warshall (PHP)

Algoritma Dijkstra, dinamai menurut penemunya, Edsger Dijkstra, adalah sebuah algoritma rakus (greedy algorithm) dalam memecahkan permasalahan jarak terpendek (shortest path problem) untuk sebuah graf berarah (directed graph) dengan bobot-bobot sisi (edge weights) yang bernilai tak-negatif.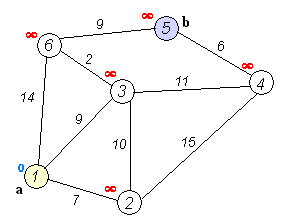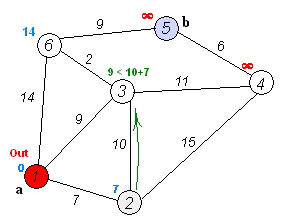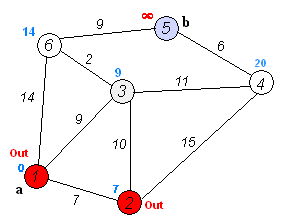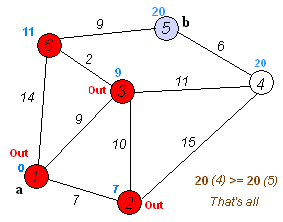
Misalnya, bila vertices dari sebuah graf melambangkan kota-kota dan bobot sisi (edge weights) melambangkan jarak antara kota-kota tersebut, maka algoritma Dijkstra dapat digunakan untuk menemukan jarak terpendek antara dua kota.
Input algoritma ini adalah sebuah graf berarah yang berbobot (weighted directed graph) G dan sebuah sumber vertex s dalam G dan V adalah himpunan semua vertices dalam graph G.
Setiap sisi dari graf ini adalah pasangan vertices (u,v) yang melambangkan hubungan dari vertex u ke vertex v.
Algoritma Floyd-Warshal
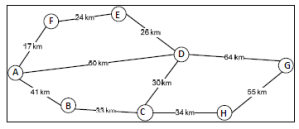
Algoritma Floyd-Warshall memiliki input graf berarah dan berbobot (V,E), yang berupa daftar titik (node/vertex V) dan daftar sisi (edge E). Jumlah bobot sisi-sisi pada sebuah jalur adalah bobot jalur tersebut. Sisi pada E diperbolehkan memiliki bobot negatif, akan tetapi tidak diperbolehkan bagi graf ini untuk memiliki siklus dengan bobot negatif. Algoritma ini menghitung bobot terkecil dari semua jalur yang menghubungkan sebuah pasangan titik, dan melakukannya sekaligus untuk semua pasangan titik.
Contoh :
Dari Titik F Menuju Titik  C ada berapa cara :
(|F|A|B|C) —>91Km
(|F|A|D|C) —>107Km
(|F|A|F|E|D|C) —>114Km
(|F|A|F|E|D|C) —>114Km
(|F|E|D|C) —>80Km
(|F|E|D|C) —>80Km
Nah, dengan algoritma Flody ini , kita dapat mendapatkan informasi yang sedemikian rupa untuk kita timbang dan menentukan jalur yang paling efisien.
PERBEDAAN
1. Algoritma Dijkstra yang menerapkan prinsip greedytidak selalu berhasil memberikan solusi optimumuntuk kasus penentuan lintasan terpendek (single pairshortest path).
2. Algoritma Floyd-Warshall yang menerapkanpemrograman dinamis lebih menjamin keberhasilanpenemuan solusi optimum untuk kasus penentuanlintasan terpendek (single pair shortest path).
Nah.. Kemudian apa sie kegunaan kedua algoritma tersebut ? ya.. mereka digunaka untuk memabntu dalam menetukan keputusan, manakah yang paling cepat dan mana yang paling efisien, dengan demikian algoritma tersebtu dapat kita gunakan dalam salah satu contoh PPC. dimana kita dapat menentukan waktu, titik kritis dan macam sebagainya.
contoh contoh pengaplikasiannya
1. Himpunan kandidat, C
Himpunan ini berisi elemen-elemen yang memiliki peluang untuk membentuk solusi. Pada persoalan lintasan terpendek dalam graf, himpunan kandidat ini  adalah himpunan simpul pada graf tersebut.
2.Himpunan solusi, SHimpunan ini berisi solusi dari permasalahan yangdiselesaikan dan elemennya terdiri dari elemendalam himpunan kandidat namun tidak semuanyaatau dengan kata lain himpunan solusi ini adalahupabagian dari himpunan kandidat.
3. Fungsi seleksiFungsi seleksi adalah fungsi yang akan memilihsetiap kandidat yang yang memungkinkan untukmenghasilkan solusi optimal pada setiap langkahnya.
4. Fungsi kelayakanFungsi kelayakan akan memeriksa apakah suatukandidat yang telah terpilih (terseleksi) melanggarconstraint atau tidak. Apabila kandidat melanggarconstraint maka kandidat tidak akan dimasukkan kedalam himpunan solusi.
5. Fungsi objektifFungsi objektif akan memaksimalkan ataumeminimalkan nilai solusi. Tujuannya adalahmemilih satu saja solusi terbaik dari masing-masinganggota himpunan solusi.

Komentar

Posting Komentar

Postingan populer dari blog ini

BAHASA INDONESIA 1 (Kalimat Efektif)

KALIMAT EFEKTIF Kalimat efektif adalah kalimat yang memiliki kemampuan untuk menimbulkan kembali gagasan-gagasan pada pikiran pendengar atau pembaca seperti gagasan yang ada pada pikiran pembicara atau penulis. Sehingga dalam penyampaian pesan dapat diterima dengan baik dan lebih mudah dimengerti.. Untuk mendapatkan kalimat yang efektif harus memenuhi beberapa syarat sebagai berikut : 1). Keterpaduan Yang dimaksud dengan keterpaduan (koherensi) adalah terjadinya hubungan yang padu antara unsure - unsur pembentuk kalimat. Yang termasuk unsure pembentuk kalimat adalah kata, frasa, klausa, tanda baca, dan fungsi sintaks S-O-P-Pel-Ket. Beberapa kriteria yang harus diperhatikan : 1. Kalimat tidak bertele - tele harus sistematis. 2. Kalimat yang padu menggunakan pola aspek - agen - verbal atau aspek - verbal - pasien. ·    Surat itu sudah saya baca. ·    Saya sudah membaca surat itu. 3. Diantara predikat kata kerja dan objek penderita tidak disisipkan kata darip
Baca selengkapnya

Mesin Turing

Gambar
Jauh sebelum lahirnya program komputer, Alan Turing pada tahun 1936 telah mengeluarkan gagasannya berupa model mesin abstrak sebagai alat mekanik untuk mengerjakan prosedur yang efektif. Model ini disebut Mesin Turing . Mesin turing dapat diadaptasi untuk mensimulasi logika dari setiap algoritma oleh karena itu cara kerja mesin turing adalah ekivalen dengan cara kerja komputer sekarang ini dan mesin turing juga ekivalen dengan problema komputasi matematika. Mesin turing tidak ditujukan sebagai teknologi komputasi praktis tetapi lebih sebagai eksperimen pemikiran yang mewakili sebuah mesin komputasi. Mesin turing membantu para ilmuan komputer memahami batas-batas komputasi mekanis.             Sebagai input dari mesin turing adalah kata atau untai atas suatu alfabet T. Mesin turing berhenti dengan keadaan menerima atau menolak untai. Kadang-kadang terjadi pula perulangan atau looping tak terhingga. Keterangan : ·         -  Tape : Tempat diletakannya i
Baca selengkapnya

Algoritma Dijkstra

Gambar
Algoritma Dijkstra , (dinamai menurut penemunya, seorang ilmuwan komputer, Edsger Dijkstra ), adalah sebuah algoritma rakus ( greedy algorithm ) yang dipakai dalam memecahkan permasalahan jarak terpendek ( shortest path problem ) untuk sebuah graf berarah ( directed graph ) dengan bobot-bobot sisi ( edge weights ) yang bernilai tak-negatif. Misalnya, bila vertices dari sebuah graf melambangkan kota-kota dan bobot sisi ( edge weights ) melambangkan jarak antara kota-kota tersebut, maka algoritma Dijkstra dapat digunakan untuk menemukan jarak terpendek antara dua kota. Input algoritma ini adalah sebuah graf berarah yang berbobot ( weighted directed graph ) G dan sebuah sumber vertex s dalam G dan V adalah himpunan semua vertices dalam graph G . Setiap sisi dari graf ini adalah pasangan vertices ( u , v ) yang melambangkan hubungan dari vertex u ke vertex v . Himpunan semua tepi disebut E . Bobot ( weights ) dari semua sisi dihitung dengan fungsi w : E → [0, ∞)
Baca selengkapnya